Una aclaratoria con base en lo
señalado en la pág. 184 de la décima lección del libro de segundo año de la
colección Bicentenario.
El profesor de Matemática, cuando trabaja las
lecciones que tienen que ver o están relacionadas con o necesitan usar las
operaciones aritméticas debe tener claro tres aspectos:
1) La Definición Matemática de las
Operaciones Aritméticas desde la matemática como Ciencia
2) Los Modelos de las Operaciones
Aritméticas que se enseñan
3) Los Algoritmos de las Operaciones Aritméticas
Recordemos que la adición se define como una
función f:AxAàA con A perteneciente a un conjunto numérico
cualquiera (N, Z, Q, R o C) donde f(a+b)=c con a, b, c pertenecientes a un conjunto numérico A; de igual manera se definen el resto de funciones con
las restricciones del caso de acuerdo al conjunto numérico en el que se esté
trabajando.
Los modelos didácticos usados para la
comprensión de las operaciones deben proporcionar elementos, desde la matemática,
que contribuyan a la formación de los conceptos adecuados.
Es por ello, que, por ejemplo, la adición
repetida en la educación secundaria o media general sería poco útil para el
estudio de estas operaciones en los conjuntos Q, R y C. Es mucho más enriquecedor el modelo
de área o plano cartesiano, tal como se usa en la página 102 y 103 de la sexta
lección del libro de primer año de la colección Bicentenario.
Ahora bien, si se desea estudiar las
propiedades de la potenciación, como de cualquier otra operación, se deben
estudiar y analizar de manera conjunta la operación y su operación inversa,
noción esta que será de utilidad en el álgebra, despeje de ecuaciones e
inecuaciones.
Esto, además, debido a que todo
proceso de la vida real, que se pueda analizar o modelar con matemática, se le
puede definir su proceso en reversa, para ello es importante comprender la
relación entre las operaciones con el fin de poder enriquecer el análisis de
cualquier proceso que se estudie: almacenaje, inventarios, insumos, crecimiento
poblacional y un largo etc.
Por ejemplo, ingreso o salida de insumos o
combinación de insumos para la preparación de productos en una fábrica de
alimentos
Proceso
(operación)
|
Proceso
Inverso
(Operación
Inversa)
|
Adición
|
Sustracción
|
operación que permite
calcular el valor de la suma
|
operación que permite
calcular el valor de un sumando
|
Si se usan 2,25Kg de guayaba
y medio kilo de azúcar, ¿cuántos kilos
de concentrado de guayaba se obtienen?
|
Para preparar 2,75 kilos de concentrado de guayaba, si se usan dos
kilos y un cuarto de guayabas, ¿cuántos kilos de azúcar se requieren?
|
Por ejemplo, análisis de movilización de pasajeros en funiculares
Proceso
(operación)
|
Proceso
Inverso
(Operación
Inversa)
|
Multiplicación
|
División
|
operación que permite
calcular el valor del producto
|
operación que permite
calcular el valor de un factor
|
6x8=48
|
48÷6=8
|
Si seis funiculares en una
hora pico viajan llenos, ¿cuántos pasajeros transportan?
|
Si se trasladan hasta Hornos
de Cal 48 pasajeros y los funiculares viajaron siempre con seis pasajeros,
¿cuántos funiculares se usaron para el traslado?
|
Por ejemplo, análisis de crecimiento poblacional
donde a es la base; n el exponente y b la potencia
Acá
debemos recordar que la potenciación tiene dos operaciones inversas
Operación
|
Operación
inversa
|
operación que permite calcular el valor de la base
|
|
operación que permite calcular el valor de la potencia
|
|
operación que permite calcular el valor del exponente
|
Proceso
(operación)
|
Proceso
Inverso
(Operación
Inversa)
|
Potenciación
|
logaritmización
|
El crecimiento de una
población de Drosophila
melanogaster, también llamada mosca de la fruta, se puede modelar con
la función f(x)=2x, ¿cuántos elementos se estima que tendrá dicha
población en determinado espacio al cabo de 5 meses?
|
Si en un almacén de
frutas se establece que la población de Drosophila melanogaster no puede exceder el número de 32 individuos
por metro cúbico, ¿cada cuánto tiempo
se debe fumigar para controlar la población de insectos?
|
Propiedades
de la Potenciación y Logaritmización
Completa la
tabla con las otras propiedades




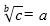




No hay comentarios:
Publicar un comentario